概述
数学是笔者的短板,最近一直在积极恶补数学,重新学习了微积分中的泰勒展开式,对其有了一点简单的理解,所以记录在这里。
简单介绍
泰勒展开式是一个在函数某点对函数进行近似的方法,在几何图形上来理解就是泰勒展开式的曲线与原函数的曲线的拟合。展开式的项是无穷多的,随着项的增加拟合的程度就越好。
看下面的图是 e^x 与其4阶泰勒展示的曲线的曲线,我们可以看到拟合程度很高。
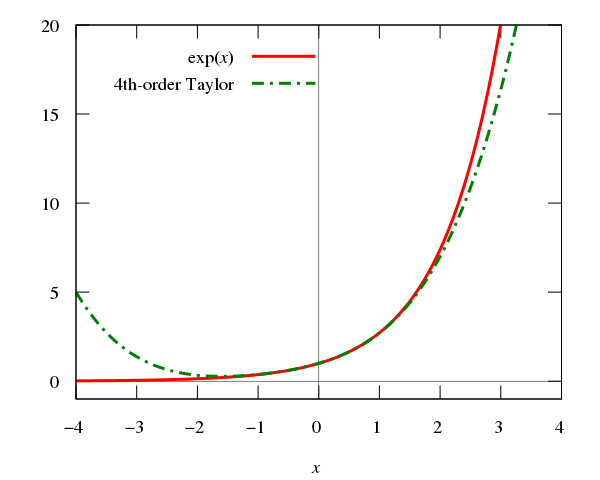
下面通过一个数据拟合的问题,来理解下泰勒展开式。
在给定一堆二位的数据,即对应二维平面上的点,我们需要根据数据的特点来对函数形式进行假设,因为假设不同,通过最小二乘法后,是可以获得不同的结果的,即不同的曲线。假设的函数的形式一般来说都是 x、x^2、x^3 … x^n 这样的添加,项越多,曲线与现有数据的拟合程度就可以更高,就可能出现过拟合的情况。
这个特点与泰勒展开式在形式上是非常相似的,泰勒展开式也是随着项越多,拟合程度越好。
用程序计算 sin
在计算机中,我们确实可以使用泰勒展开式来计算,因为其形式非常适合迭代计算,在误差较小的时候,停止即可。
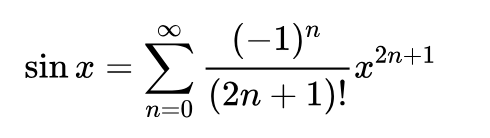
def factorial(n):
if n in (0, 1):
return 1
else:
return n * factorial(n - 1)
def sin(x):
i = 1
f = 1.0
sign = 1
sum = x
result = sum
while abs(sum) > 1e-10:
sign = -sign
f = f * (i + 1) * (i + 2)
i += 2
sum = sign * ((x ** i) / f)
result += sum
return result
if __name__ == '__main__':
import math
print sin(10)
print math.sin(10)
